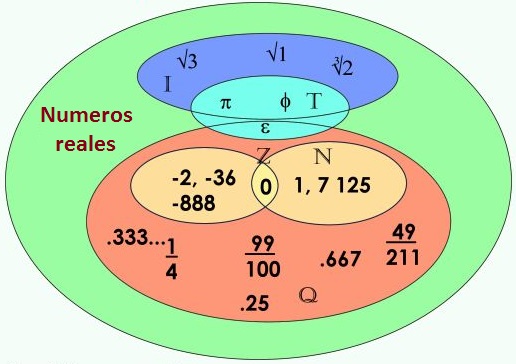
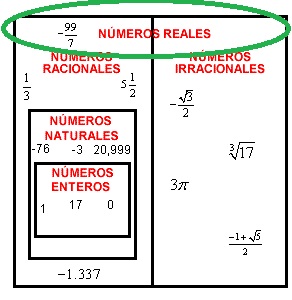
Llamamos números reales a todos los números tanto positivos (1, 2, 3, 4, 5...) como los que tienen un signo negativo (-1, -2, -3, -4, -5...). Se componen de números racionales y números irracionales. Los números racionales pueden ser enteros o fracciones. Los números irracionales por el contrario se caracterizan porque no pueden expresarse en fracciones.

Ejemplos de números reales
- 4/5: es un número real, de los que llamamos racionales porque se puede expresar en una fracción.
- 10: es un número real pero en esta ocasión no está dividido por otro número si no que es entero.
- Raíz cuadrada de 9: en este caso es un número real pero irracional, representa un número que un número ilimitado de decimales que no se repiten de manera periódica. Generalmente cuando expresamos este tipo de números, lo solemos hacer añadiendo 3 o 4 decimales y posteriormente el símbolo de puntos suspensivos que significan continuidad.
- El número cero "0" también está dentro del conjunto de números reales.
Los números reales nacieron en el antiguo Egipto, aproximadamente sobre el año 1.000 antes de Cristo, para dar respuesta a cálculos cada vez más complejos y que necesitaban más exactitud, como por ejemplo los cálculos necesarios para hacer ciertas construcciones antiguas en las que ya no servían las aproximaciones. Los egipcios se vieron en la necesidad de realizar operaciones para obtener resultados precisos y fiables que les ahorraran tiempo y espacio. Pero fueron los griegos y en especial Pitágoras quienes entendieron el verdadero valor de los números reales.
Los números reales se representan con la letra R y gracias a ellos podemos realizar la mayoría de las operaciones matemáticas que se nos ocurran: sumar, restar, dividir, multiplicar, hacer raíces cuadradas... las únicas operaciones que no se pueden calcular con los números reales son la división de un número entre cero ya que no podemos dividir un número entre nada, no tiene ningún sentido. Además tampoco se puede realizar la operación de coger raíces pares de números negativos.
También son considerados números reales algunos símbolos matemáticos como el número Pi y el número e. Este tipo de números reales se consideran trascedentes.
Los números reales se representan geométricamente a través de una línea recta, dividida por puntos o líneas en las que a una línea o punto, generalmente situado en medio de la recta, se le asigna el número 0 y posteriormente a la siguiente línea por la derecha se le asignará el número 1, y la siguiente línea por la izquierda se le asignará el número menos 1 y así sucesivamente.
Más ejemplos de números reales